–ė–Ē–ó 1.1 –†—Ź–Ī—É—ą–ļ–ĺ

–í—Ā–Ķ –≥–ĺ—ā–ĺ–≤—č–Ķ –≤–į—Ä–ł–į–Ĺ—ā—č —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ –ļ –ė–Ē–ó 1.1 –†—Ź–Ī—É—ą–ļ–ĺ –ź.–ü. –í—č–Ī–Ķ—Ä–ł—ā–Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ—č–Ļ –≤–į—Ä–ł–į–Ĺ—ā –ł–∑ —Ā–Ņ–ł—Ā–ļ–į.
- –í–į—Ä–ł–į–Ĺ—ā 1
- –í–į—Ä–ł–į–Ĺ—ā 2
- –í–į—Ä–ł–į–Ĺ—ā 3
- –í–į—Ä–ł–į–Ĺ—ā 4
- –í–į—Ä–ł–į–Ĺ—ā 5
- –í–į—Ä–ł–į–Ĺ—ā 6
- –í–į—Ä–ł–į–Ĺ—ā 7
- –í–į—Ä–ł–į–Ĺ—ā 8
- –í–į—Ä–ł–į–Ĺ—ā 9
- –í–į—Ä–ł–į–Ĺ—ā 10
- –í–į—Ä–ł–į–Ĺ—ā 11
- –í–į—Ä–ł–į–Ĺ—ā 12
- –í–į—Ä–ł–į–Ĺ—ā 13
- –í–į—Ä–ł–į–Ĺ—ā 14
- –í–į—Ä–ł–į–Ĺ—ā 15
- –í–į—Ä–ł–į–Ĺ—ā 16
- –í–į—Ä–ł–į–Ĺ—ā 17
- –í–į—Ä–ł–į–Ĺ—ā 18
- –í–į—Ä–ł–į–Ĺ—ā 19
- –í–į—Ä–ł–į–Ĺ—ā 20
- –í–į—Ä–ł–į–Ĺ—ā 21
- –í–į—Ä–ł–į–Ĺ—ā 22
- –í–į—Ä–ł–į–Ĺ—ā 23
- –í–į—Ä–ł–į–Ĺ—ā 24
- –í–į—Ä–ł–į–Ĺ—ā 25
- –í–į—Ä–ł–į–Ĺ—ā 26
- –í–į—Ä–ł–į–Ĺ—ā 27
- –í–į—Ä–ł–į–Ĺ—ā 28
- –í–į—Ä–ł–į–Ĺ—ā 29
- –í–į—Ä–ł–į–Ĺ—ā 30
–ě–Ī—Ä–į–∑–Ķ—Ü —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ė–Ē–ó 1.1
–ě–Ī—Ä–į–∑–Ķ—Ü —ā–ł–Ņ–ĺ–≤–ĺ–≥–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ė–Ē–ó 1.1 –ļ —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ—É –†—Ź–Ī—É—ą–ļ–ĺ –ź.–ü. –ü–ĺ –ī–į–Ĺ–Ĺ–ĺ–ľ—É –Ņ—Ä–ł–ľ–Ķ—Ä—É –≤—č —Ā–į–ľ–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ľ–ĺ–∂–Ķ—ā–Ķ —Ä–Ķ—ą–ł—ā—Ć —Ā–≤–ĺ—Ď –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ—Ć–Ĺ–ĺ–Ķ –ī–ĺ–ľ–į—ą–Ĺ–Ķ–Ķ –∑–į–ī–į–Ĺ–ł–Ķ –Ņ–ĺ —ā–Ķ–ľ–Ķ «–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ–ł. –ú–į—ā—Ä–ł—Ü—č. –°–ł—Ā—ā–Ķ–ľ—č –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č—Ö –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–ł».
–ó–į–ī–į–Ĺ–ł–Ķ 1
–Ē–Ľ—Ź –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ź:
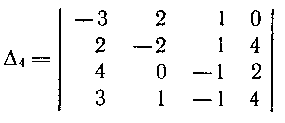
–į) —Ä–į–∑–Ľ–ĺ–∂–ł–≤ –Ķ–≥–ĺ –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ 1-–Ļ —Ā—ā—Ä–ĺ–ļ–ł;
–Ī) —Ä–į–∑–Ľ–ĺ–∂–ł–≤ –Ķ–≥–ĺ –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ā—ā–ĺ–Ľ–Ī—Ü–į;
–≤) –Ņ–ĺ–Ľ—É—á–ł–≤ –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ĺ—É–Ľ–ł –≤ –Ņ–Ķ—Ä–≤–ĺ–Ļ —Ā—ā—Ä–ĺ–ļ–Ķ.
–Ě–į—Ö–ĺ–ī–ł–ľ.
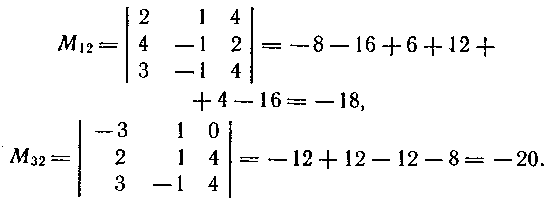
–ź–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł–Ķ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ a12, a32 —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č:
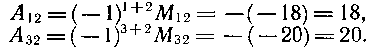
–į) –í—č—á–ł—Ā–Ľ–ł–ľ.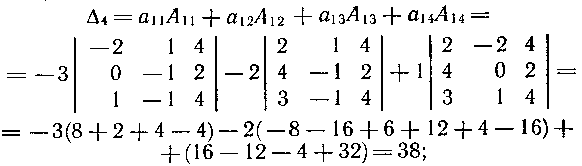
–Ī) –†–į–∑–Ľ–ĺ–∂–ł–ľ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ā—ā–ĺ–Ľ–Ī—Ü–į:
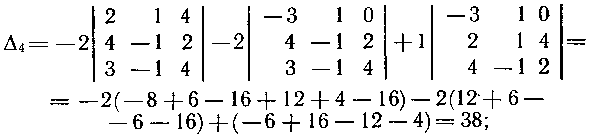
–≤) –í—č—á–ł—Ā–Ľ–ł–ľ Δ4, –Ņ–ĺ–Ľ—É—á–ł–≤ –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ĺ—É–Ľ–ł –≤ –Ņ–Ķ—Ä–≤–ĺ–Ļ —Ā—ā—Ä–ĺ–ļ–Ķ. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ 10 –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ (—Ā–ľ. § 1.1 —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ–į –†—Ź–Ī—É—ą–ļ–ĺ). –£–ľ–Ĺ–ĺ–∂–ł–ľ —ā—Ä–Ķ—ā–ł–Ļ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ü –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ź –Ĺ–į 3 –ł –Ņ—Ä–ł–Ī–į–≤–ł–ľ –ļ –Ņ–Ķ—Ä–≤–ĺ–ľ—É, –∑–į—ā–Ķ–ľ —É–ľ–Ĺ–ĺ–∂–ł–ľ –Ĺ–į -2 –ł –Ņ—Ä–ł–Ī–į–≤–ł–ľ –ļ–ĺ –≤—ā–ĺ—Ä–ĺ–ľ—É. –Ę–ĺ–≥–ī–į –≤ –Ņ–Ķ—Ä–≤–ĺ–Ļ —Ā—ā—Ä–ĺ–ļ–Ķ –≤—Ā–Ķ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—č, –ļ—Ä–ĺ–ľ–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ, –Ī—É–ī—É—ā –Ĺ—É–Ľ—Ź–ľ–ł. –†–į–∑–Ľ–ĺ–∂–ł–ľ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č–Ļ —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ –Ņ–Ķ—Ä–≤–ĺ–Ļ —Ā—ā—Ä–ĺ–ļ–ł –ł –≤—č—á–ł—Ā–Ľ–ł–ľ –Ķ–≥–ĺ:
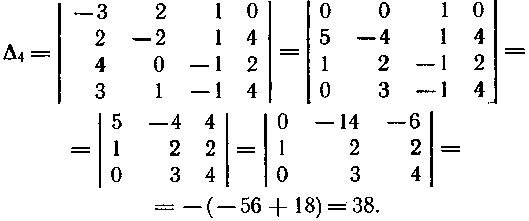
–í –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į –Ņ–ĺ–Ľ—É—á–ł–Ľ–ł –Ĺ—É–Ľ–ł –≤ –Ņ–Ķ—Ä–≤–ĺ–ľ —Ā—ā–ĺ–Ľ–Ī—Ü–Ķ –Ņ–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤—É 10 –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ.
–ó–į–ī–į–Ĺ–ł–Ķ 2
–Ē–į–Ĺ—č –ī–≤–Ķ –ľ–į—ā—Ä–ł—Ü—č:
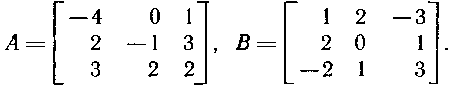
–Ě–į–Ļ—ā–ł: –į) –ź–í; –Ī) –í–ź; –≤) –ź-1; –≥) –ź–ź-1; –≥) –ź-1;–ź.
–ü—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –ź–í –ł–ľ–Ķ–Ķ—ā —Ā–ľ—č—Ā–Ľ, —ā–į–ļ –ļ–į–ļ —á–ł—Ā–Ľ–ĺ —Ā—ā–ĺ–Ľ–Ī—Ü–ĺ–≤ –ľ–į—ā—Ä–ł—Ü—č –ź —Ä–į–≤–Ĺ–ĺ —á–ł—Ā–Ľ—É —Ā—ā—Ä–ĺ–ļ –ľ–į—ā—Ä–ł—Ü—č –í. –Ě–į—Ö–ĺ–ī–ł–ľ –ľ–į—ā—Ä–ł—Ü—É –°=–ź–í, —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—č –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ cij=ai1b1j+ai2b2j+ai3b3j+...+ainbnj.
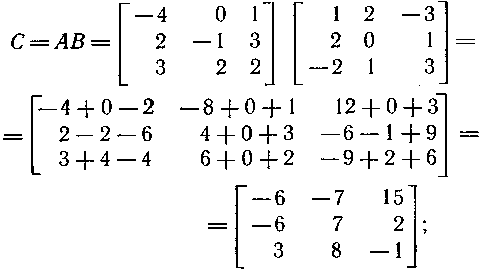
–Ī) –í—č—á–ł—Ā–Ľ–ł–ľ:
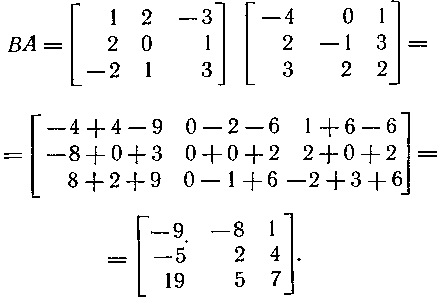
–ě—á–Ķ–≤–ł–ī–Ĺ–ĺ, —á—ā–ĺ –ź–í=–í–ź.
–ě–Ī—Ä–į—ā–Ĺ–į—Ź –ľ–į—ā—Ä–ł—Ü–į –ź-1 –ľ–į—ā—Ä–ł—Ü—č –ź –ł–ľ–Ķ–Ķ—ā –≤–ł–ī (—Ā–ľ. —Ą–ĺ—Ä–ľ—É–Ľ—É (1.1) –≤ —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ–Ķ)
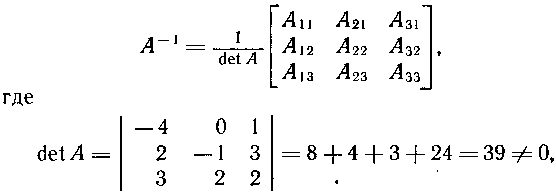
—ā.–Ķ. –ľ–į—ā—Ä–ł—Ü–į –ź - –Ĺ–Ķ–≤—č—Ä–ĺ–∂–ī–Ķ–Ĺ–Ĺ–į—Ź, –ł, –∑–Ĺ–į—á–ł—ā, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ľ–į—ā—Ä–ł—Ü–į –ź-1. –Ě–į—Ö–ĺ–ī–ł–ľ:

–≥) –ė–ľ–Ķ–Ķ–ľ:
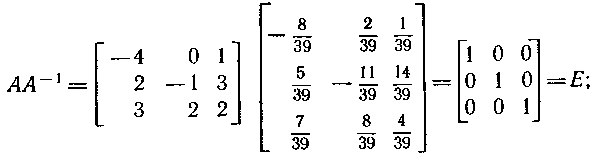
–ī) –ė–ľ–Ķ–Ķ–ľ:
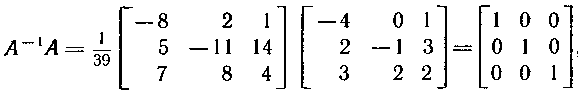
idz-ryabushko.ru/online-shop/ - –ě–Ĺ–Ľ–į–Ļ–Ĺ –ľ–į–≥–į–∑–ł–Ĺ –≥–ĺ—ā–ĺ–≤—č—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ. –Ē–Ľ—Ź —ā–Ķ—Ö –ļ—ā–ĺ —Ö–ĺ—á–Ķ—ā –ļ—É–Ņ–ł—ā—Ć –ė–Ē–ó –†—Ź–Ī—É—ą–ļ–ĺ —Ā —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ.