ИДЗ 1.2 Рябушко

Образец решения ИДЗ 1.2

Образец типового решения ИДЗ 1.2 к сборнику Рябушко А.П. По данному примеру вы самостоятельно можете решить своё индивидуальное домашнее задание по теме «Определители. Матрицы. Системы линейных алгебраических уравнении».

Задание 1

Дана система линейных неоднородных алгебраических уравнений

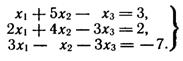
Проверить, совместна ли эта система, и в случае совместности решить ее:

• а) по формулам Крамера;
• б) с помощью обратной матрицы (матричным методом);
• в) методом Гаусса.

► Совместность данной системы проверим по теореме Кронекера — Капелли. С помощью элементарных преобразований найдем ранг матрицы

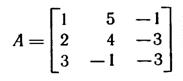
данной системы и ранг расширенной матрицы .

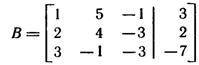
Для этого умножим первую строку матрицы В на -2 и сложим со второй, затем умножим первую строку на -3 и сложим с третьей, поменяем местами второй и третий столбцы. Получим:

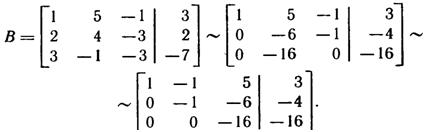
Следовательно, rang А = rang В - 3 (т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.

а) По формулам Крамера (1.17)

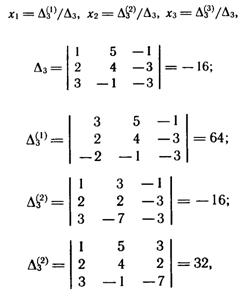
находим: x₁=64/(-16)=-4, x₂=-16/(-16)-1, x₃ = 32/( -16) = -2;

б) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме 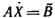. Решение системы в матричной форме имеет вид 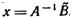. По формуле (1.11) находим обратную матрицу А^-1(она существует, так как

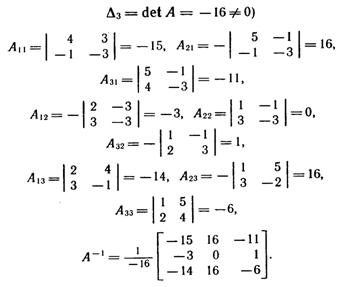
Решение системы:

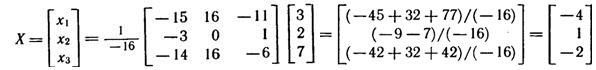
Итак, x₁ = -4, x₂=1, x₃=-2;

в) Решим систему методом Гаусса. Исключим x₁ из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:

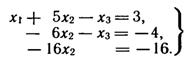
Из полученной системы находим x₁ = -4, x₂=1, x₃=-2.

Задание 2

Дана система линейных неоднородных алгебраических уравнений.

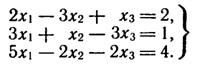
Проверить, совместна ли эта система, и в случае совместности решить ее:

• а) по формулам Крамера;
• б) с помощью обратной матрицы (матричным методом);
• в) методом Гаусса.

► Проверяем совместность системы с помощью теоремы Кронекера — Капелли. В расширенной матрице

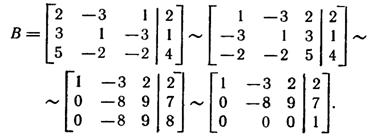
Теперь ясно, что rang A = 2, rang В = 3. Согласно теореме Кронекера — Капелли, из того, что rang А ≠ rang В, следует несовместность исходной системы.

Задание 3

Решить однородную систему линейных алгебраических уравнений

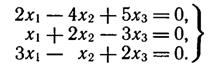
► Определитель системы
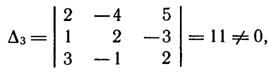
поэтому система имеет единственное нулевое решение x₁=x₂=x₃ = 0.

Задание 4

Решить однородную систему линейных алгебраических уравнений

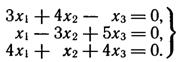
► Так как

то система имеет бесчисленное множество решений. Поскольку rang А = 2, n = 3, возьмем любые два уравнения системы (например, первое и второе) и найдем ее решение. Имеем:

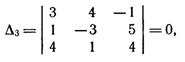
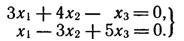
Так как определитель из коэффициентов при неизвестных x₁ и x₂ не равен нулю, то в качестве базисных неизвестных возьмем x₁ и x₂ (хотя можно брать и другие пары неизвестных) и переместим члены с x₃ в правые части уравнений:

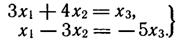
Решаем последнюю систему по формулам Крамера (1.17):

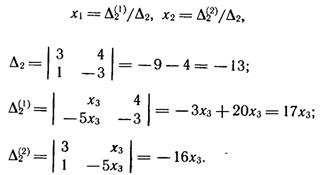
Отсюда находим, что x₁ = -17х₃/13, х₂=16х₃/13. Полагая x₃=13k, где k — произвольный коэффициент пропорциональности, получаем решение исходной системы: х₁ = -17k, х₂ = 16k, x₃ = 13k